为什么“负负得正”?
作者 | 大小吴
来源 | 大小吴的数学课堂
(-1)×(-1) = 1 是每一个上过中学的人都熟知的事实,但是即便是非常简单的“负负得正”,你有想过这是为什么吗?今天大小吴就和大家来探讨一下这件事。
1 司汤达的疑问
将财产记为正数,负债记为负数对于普通人来说确实是一件易于理解的事,这种记录方式始于7世纪的印度,它适用于加减法的运算,比如,本来有 10 元,支出 12 元,对应的算式是 10 - 12 = -2 。这里的对应的实际含义是“负债 2 元”。
然而,当要对其进行乘除法的时候,就会出现某些匪夷所思的问题,在12世纪,印度天文学家巴斯卡拉这样说道:“财产和财产的乘积,债金和债金的乘积均为财产,财产和债金的乘积则是债金。”根据他的说法,就有 债金×债金 = 财产 。这个公式是什么意思呢?恐怕无人能够理解。18世纪的大数学家欧拉在其著作《代数学入门》采用过同样的说明方法,这让许多学习数学的人在初遇负数相乘问题的时候感到一头雾水。

司汤达(1783~1842)
《红与黑》的作者,19世纪法国批判现实主义作家司汤达在其年少时酷爱数学,但他同样也困惑于“负负得正”问题,他在其自传中这样写道:
似乎是由于年少的单纯,使我认为在数学中是不可能有虚假的,然而当了解了谁也没加证明的(负×负)=(正)时,该怎么办才好呢(这是代数学的基础之一)。当考虑某人有负的借款时,为何 1 万法郎的借款乘以 500 法郎借款,就会变成 500 万法郎的财产了呢……
实际上,司汤达提出了每一个学习代数的人都必然会提出的问题,即为什么“负负得正”?该如何直观地理解这件事?
2 从实际的角度
问题出在了对正负数的说明上。仔细想想,对于什么是 财产×财产,债金×债金,恐怕谁也无法说明,因为金额再乘以金额是没有实际意义的。
M·克莱因(1908-1992
对此,《古今数学思想》的作者,美国数学史家和数学教育家M·克莱因通过“负债模型”巧妙地说明了“负负得正”问题:
一个人每天欠债 5 元,从给定日期开始(比如今天)3 天后欠债 15 元。如果将 5 元的负债记作 -5 ,那么“每天欠债 5 元,欠债 3 天”可以用数学来表达:(-5)×3 = -15 。
同样地,每天欠债 5 元,考虑这个人 3 天前的财产,那么就应该比今天的财产多 15 元。如果我们用 -3 表 示 3 天前,用 -5 表示每天欠债,那么 3 天前他的财产情况就可以表示为 (-5)×(-3) = +15 。
受此启发,我们也可以举出“批阅试卷”的例子来进行说明:
如果有一次考试某同学错了一道题,扣 5 分,则将其记为,对应的算式是:(-5)×1 = -5 。
这里的 1 表示的实际含义是 1 道错题。
换个角度想,假若是老师批错了,那么很显然这位同学扣除的 5 分就会加回去了,其得分是 +5 。
1 表示老师批对,那么相对应地,则 -1 表示老师批错,对应的算式是:(-5)×(-1) = +5 。
上述两个例子是自然的,也是合乎情理的,可以帮助我们理解“负负得正”。
3 从运算逻辑的角度

4 从几何的角度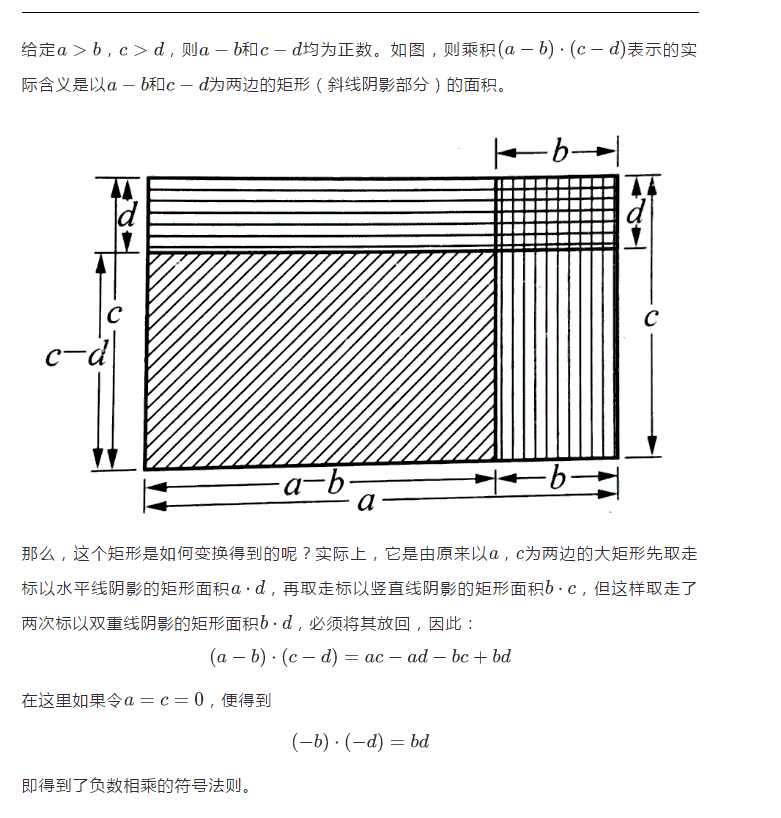
5 不能加以证明的“负负得正”

参考文献:
[1](日)远山启.数学与生活[M].吕砚山等译.人民邮电出版社,2014.
[2](美)R·柯朗,H·罗宾. 什么是数学——对思想和方法的基本研究[M].复旦大学出版社,2012.
[3](德)菲利克斯·克莱因.高观点下的初等数学(第一卷)——算术 代数 分析[M].舒湘芹等译.复旦大学出版社,2008.